• Jul 4, 2020

    Phonon contribution to resonant inelastic X-ray Scattering : package release

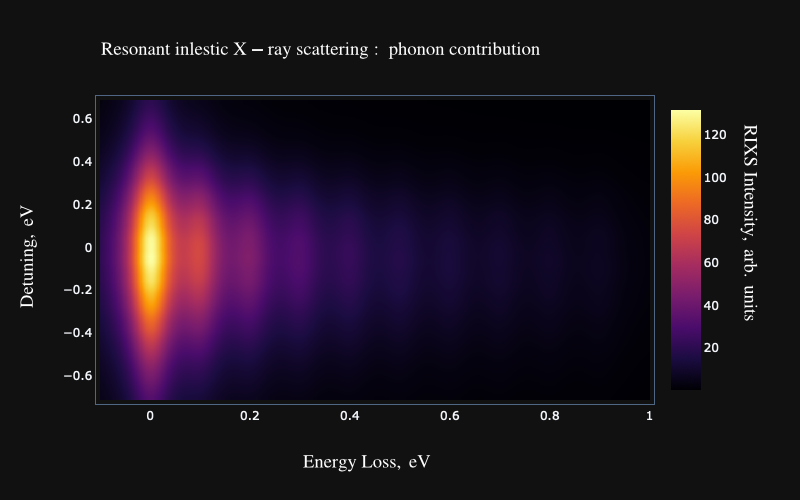
    phonon contribution in RIXS

    This package aims to create a convenient set of tools for analyzing experimental data and obtaining electron-phonon coupling values from phonon contribution to resonant inelastic X-ray scattering cross-section.

    It currently includes:

    • Model for 1D harmonic oscillator interacting with a single electronic level.
    • Model for 2D harmonic oscillator (two modes active).
    • Model for 1D harmonic oscillator, distorted and displaced in the excited state (excited-state potential energy surface (PES), differs from the ground state one).
  • Jul 1, 2020

    zsh+iterm : clever and beautiful

    x

  • Apr 25, 2020

    Launching a website with Jekyll in 8 steps

    An obvious thing to do when you just launched a blog on GitHub pages is to write about it.

    To succeed through this journey, one only needs to have a Github account, some understanding of Git and Jekyll will do the rest.

    In principle it is possible to work on remote repository without even installing Jekyll but since it is a genuinely useful and convenient tool for managing your website, so I’d recommend having it.

  • Apr 20, 2020

    Quantum Computing : Modeling Bell's (CHSH) inequality with Qiskit

    source on github

    CHSH correlation function (S) vs relative angle between detectors ($\theta$).

    CHSH correlation function vs relative angle between detectors (\theta).

    Formulation

    From the classical point of view, the following inequality holds for any local hidden variable theory \begin{equation} |S|<2 \ . \end{equation} Here \begin{equation} S=E(\textbf{AB})-E(\textbf{AB’})+E(\textbf{A’B’})+E(\textbf{A’B}) \ , \end{equation} where \(E(\textbf{AB})\) - is a correlation function (for example, spin-spin correlation function) between two points on different sides of the source and arbitary unit vectors (\(\textbf{A}\), \(\textbf{B}\)) specify orientations of the linear detectors.

    However, within the framework of the quantum mechanics (QM), things are different. QM states that there are specific configurations of the experiment for which S becomes greater than two.

    Thus ineq. 1 appears to be an important and convenient test in favor of one or another theory. So far, the experiment (despite some challenges) confirms prediction of the quantum mechanic and, consequently, the non-locality of our nature.